Leetcode-Greedy Algorithm
Reference: Link
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage with the intent of finding a global optimum.
455. Assign Cookies (Easy)
At first, we need to sort two arrays, because we want to use small cookie to content the child who is easily content. If we can use current cookie to content current child, we move to next child. Otherwise, we move to next cookie.
Time complexity is O(mlogm+nlogn). Space complexity is O(1). Here is the link.
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int ans = 0;
for(int i = 0,j=0;i<g.length && j<s.length;i++){
while(j<s.length && s[j]<g[i])j++;
if(j==s.length)break;
ans++;
j++;
}
return ans;
}
435. Non-overlapping Intervals (Medium)
At first, we still need to sort intervals. We sort intervals according to their end time. Then we iterate intervals. In each step, we update end time. If we find an overlap interval, we plus 1 to answer and update start time to make sure our global interval is small enough. We want the minimum number, so we make sure our global interval is small enough.
Time complexity is O(nlogn). Space complexity is O(1). Here is the link.
public int eraseOverlapIntervals(int[][] intervals) {
if(intervals.length==0)return 0;
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
int ans = 0;
int end = intervals[0][1];
for(int i =1;i<intervals.length;i++){
if(intervals[i][0]<end){
ans++;
}
else{
end = intervals[i][1];
}
}
return ans;
}
452. Minimum Number of Arrows to Burst Balloons (Medium)
This problem is exactly same as the last problem. We need to calculate the non-overlap intervals. But remember, sometimes we may have a very large number like the test case [[-2147483646,-2147483645],[2147483646,2147483647]]. Inside our override compare function, if we decide to use a1[1]-a2[1], this will lead to an error because the result of a1[1]-a2[1] is larger than the scope of integer. So we’d better return -1, 1 or 0.
Time complexity is O(nlogn). Space complexity is O(1). Here is the link.
public int findMinArrowShots(int[][] points) {
if(points.length==0)return 0;
Arrays.sort(points, new Comparator<int[]>(){
@Override
public int compare(int[]a1, int[]a2){
if(a1[1]<a2[1])return -1;
else if(a1[1]>a2[1])return 1;
else return 0;
}
});
int high = points[0][1];
int ans = 0;
for(int i = 1;i<points.length;i++){
if(points[i][0]>high){
ans++;
high = points[i][1];
}
}
return ans+1;
}
406. Queue Reconstruction by Height(Medium)
At first, we need to sort this array. Higher people has smaller index. If two persons have same height, the person with smaller second value has smaller index. We sort people height in ascending order because the second value means the number of people in front of the person who are higher. Hence, we can ensure relative positions are right. We sort second value in descending order because the same height is also counted as the second value.
After sorting, we add all elements into a new array. When you are adding an element, their second indices are their true indices.
Time complexity is O(nlogn). Space complexity is O(n). We can reduce space complexity to O(1). We can change positions of elements in place. But this is not the core point of this problem. Here is the link.
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people,new Comparator<int[]>(){
@Override
public int compare(int[]a1,int[]a2){
return a1[0]==a2[0]?a1[1]-a2[1]:a2[0]-a1[0];
}
});
List<int[]>list = new ArrayList();
for(int[]person:people){
list.add(person[1],person);
}
return list.toArray(new int[list.size()][]);
}
We have a second solution. The center idea is same. But we can save space complexity to O(1). We don’t create a new list.
We operate the array people in place. We just move the data to the right position.
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people,new Comparator<int[]>(){
@Override
public int compare(int []a1,int[]a2){
if(a1[0]>a2[0]){
return -1;
}
else if(a1[0]<a2[0]){
return 1;
}
else{
if(a1[1]>a2[1]){
return 1;
}
else
return -1;
}
}
});
for(int i =0;i<people.length;i++){
int supposedIndex = people[i][1];
int curIndex = i;
while(supposedIndex!=i){
int[]temp = new int[]{people[i][0],people[i][1]};
people[i][0] = people[i-1][0];
people[i][1] = people[i-1][1];
people[i-1][0] = temp[0];
people[i-1][1] = temp[1];
i--;
}
i = curIndex;
}
return people;
}
121. Best Time to Buy and Sell Stock (Easy)
You need to iterate the whole array. Record the minimum price as the buying price. Update the answer when you are iterating.
Time complexity is O(n). Space complexity is O(1). Here is the link.
public int maxProfit(int[] prices) {
if(prices.length<=1)return 0;
int minPrice = prices[0];
int ans = 0;
for(int i =1;i<prices.length;i++){
ans = Math.max(ans,prices[i]-minPrice);
minPrice = Math.min(minPrice,prices[i]);
}
return ans;
}
122. Best Time to Buy and Sell Stock II (Easy)
Consider an example [a,b,c,d]. a<=b<=c<=d. The answer will be d-a = (d-c)+(c-b)+(b-a). Therefore, if we find prices[i]>prices[i-1], we add their difference into the answer.
Time complexity is O(n). Space complexity is O(1). Here is the link.
public int maxProfit(int[] prices) {
int ans = 0;
if(prices.length<=1)return 0;
int minPrice = prices[0];
for(int i =1;i<prices.length;i++){
}
return ans;
}
605. Can Place Flowers (Easy)
This problem is easy. You just need to check the previous position, current position and next position whether they are 0. And you also need to be careful about border, index = 0 and length-1.
Time complexity is O(n). Space complexity is O(1). Here is the link.
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int l = flowerbed.length;
for(int i = 0;i<l;i++){
int pre = i==0?0:flowerbed[i-1];
int next = i==l-1?0:flowerbed[i+1];
if(pre==0 && flowerbed[i]==0 && next==0){
n--;
flowerbed[i]=1;
}
if(n==0)return true;
}
return n>0?false:true;
}
665. Non-decreasing Array (Easy)
This problem doesn’t have any trick. You just need to be careful we should we should update nums[i] or nums[i+1] when nums[i]>nums[i+1]. If i == 0 & [4,2,3], we need to replace 4 with 2. If [1,4,2,3], we should replace 4 with 2. If [3,4,2,4], we should replace 2 with 4.
I did this problem again and I want to make some notes here. For this problem, we are iterating from left to right, so we are sure that nums[i-1]<=nums[i] at the left of the current index(Assume current index is k, i<=k, nums[i-1]<=nums[i]). The left of the array is always non-ascending order. If we find nums[i]>nums[i+1], we need to replace the value of nums[i] with nums[i+1], because we are not sure whether nums[i]>nums[i+2]. If we replace nums[i+1] with nums[i], we need to do one more delete. But if nums[i-1]>nums[i+1], we need to replace nums[i+1] with nums[i].
Time complexity is O(n). Space complexity is O(1). Here is the link.
public boolean checkPossibility(int[] nums) {
int cnt = 0;
for(int i =0;i<nums.length-1;i++){
if(nums[i]>nums[i+1]){
cnt++;
if(i==0||(i>0 && nums[i-1]<=nums[i+1]))nums[i] = nums[i+1];
else nums[i+1]=nums[i];
}
if(cnt>1)return false;
}
return true;
}
53. Maximum Subarray (Easy)
In this problem, we need a variable to record current sum. In each iteration, we compare nums[i] and curSum+nums[i]. Meanwhile, we update maximum answer.
Time complexity is O(n). Space complexity is O(1). Here is the link.
public int maxSubArray(int[] nums) {
if(nums.length==0) return 0;
int sum = 0;
int res = Integer.MIN_VALUE;
for(int i =0;i<nums.length;i++){
sum = Math.max(sum+=nums[i],nums[i]);
res = Math.max(res,sum);
}
return res;
}
763. Partition Labels (Medium)
The length of one part depends on the last index of each character in this part. At first, we need to record each characters’ last index in the string. And we iterate the string and update variable ‘last’. Variable ‘last’ means the last index of one part. And we also need a variable ‘start’ to record the start index of one part. If we find index i is equal to the last index, we find one part and can be added to our answer. Then we update the variable ‘start’ as index (i+1) and continue to iterate the string.
Time complexity is O(n). Space complexity is O(n). Here is the link.
public List<Integer> partitionLabels(String S) {
int[]lastIndex = new int[26];
for(int i =0;i<S.length();i++){
lastIndex[S.charAt(i)-'a'] = i;
}
int last = lastIndex[S.charAt(0)-'a'];
List<Integer>ans = new ArrayList();
int start = 0;
for(int i =0;i<S.length();i++){
if(lastIndex[S.charAt(i)-'a']>last)
last = lastIndex[S.charAt(i)-'a'];
if(i==last){
ans.add(last-start+1);
start = i+1;
}
}
return ans;
}
646. Maximum Length of Pair Chain (Medium)
We can select pairs in any order which means we can change the order of input array. Therefore, we sort the input array in ascending order according to the second value of each elements. We cannot sort according to the first value. Assume input array is [[2,4],[1,5]]. If we sort it according to the first value, it will be [[1,5],[2,4]]. Then, when we iterate it, we will consider [1,5] as the part of answer at first. But if we consider [2,4] as the part of the answer, we may get a longer length of pair chain. Therefore, we need to sort input array according to the second value. Next, we use a variable to record the last value of pair chain.
Time complexity is O(nlogn). Space complexity is O(1). Here is the link.
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs, (a, b) -> a[1] - b[1]);
int tail = pairs[0][1];
int ans = 1;
for(int i =1;i<pairs.length;i++){
if(pairs[i][0]>tail){
ans++;
tail = pairs[i][1];
}
}
return ans;
}
376. Wiggle Subsequence (Medium)
Let’s consider about nums[i] and nums[i-1]. The idea is very obvious if you draw a diagram. Loot at the below diagram. Assume nums[i]>nums[i-1].
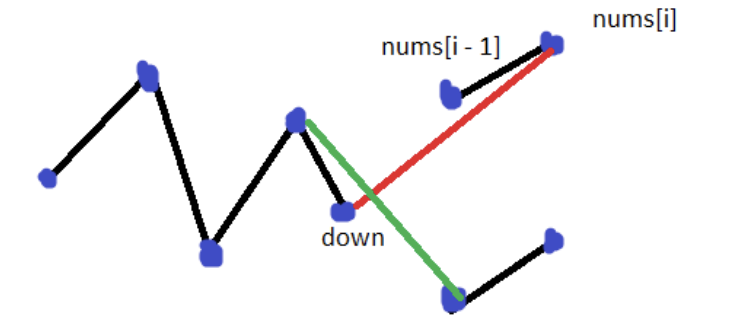
No matter the position of nums[i] and nums[i-1], the length of descend always plus 1. This also applies to nums[i]<nums[i-1].
Time complexity is O(n). Space complexity is O(1). Here is the link.
public int wiggleMaxLength(int[] nums) {
if(nums.length<2)return nums.length;
int ascend = 1;
int descend = 1;
for(int i =1;i<nums.length;i++){
if(nums[i]>nums[i-1])ascend = descend+1;
else if(nums[i]<nums[i-1])descend = ascend+1;
}
return Math.max(ascend,descend);
}