Reference: Link

LeetCode Binary Search Summary 二分搜索法小结

I think most of CSE students are very familiar with binary search. But you may see so many versions of binary search. We need to be careful about the target value, left/low value and right/high value. There are three main kinds of binary search.

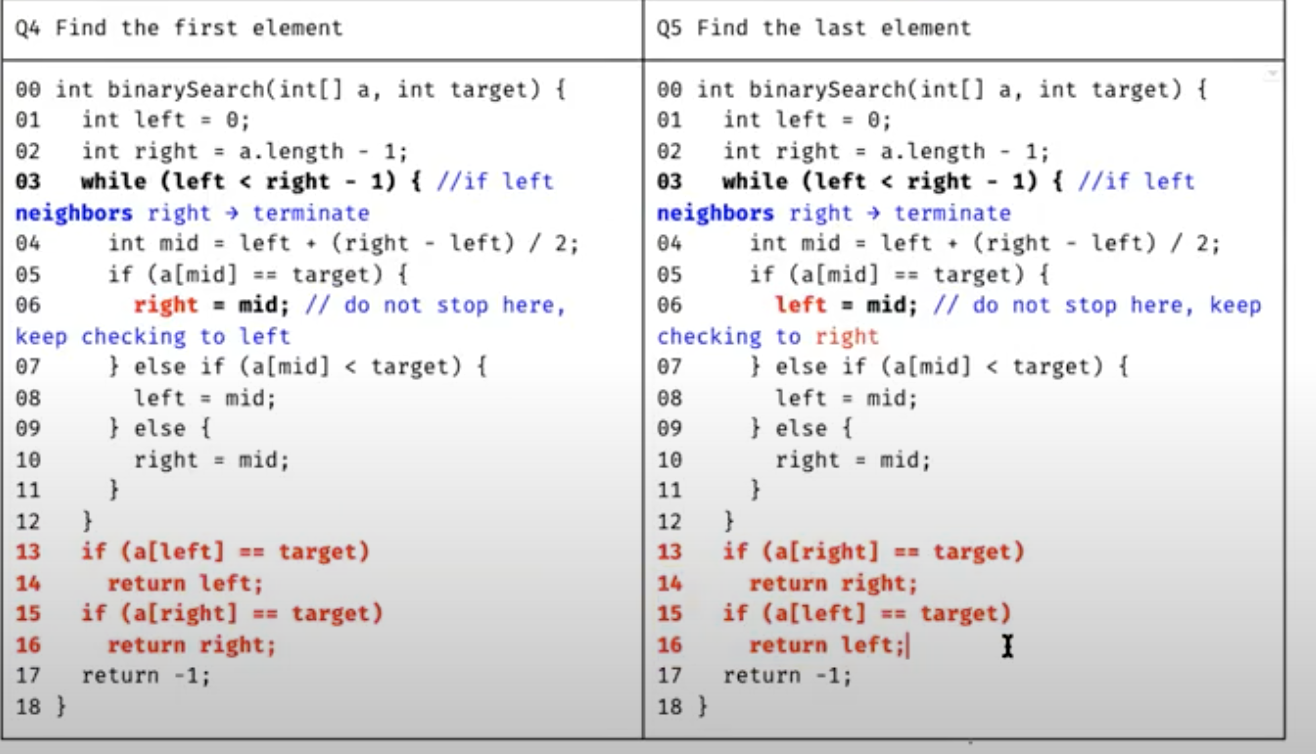
Find the value which is equal to the target value. This is the most common one. Here is the code.

 int find(int[] nums, int target) {
     int left = 0, right = nums.length-1;
     while (left <= right) {
         int mid = left + (right - left) / 2;
         if (nums[mid] == target) return mid;
         else if (nums[mid] < target) left = mid + 1;
         else right = mid-1;
     }
     return -1;
 }

Leetcode problem: Intersection of Two Arrays.

Find the first value which is not smaller than the target value/ the last value which is smaller than the target value. For this version, the target value maybe not in the array. The position we need to return is where the right pointer points. We don’t need to consider about the condition nums[mid]==target.
```
 int find(int[] nums, int target) {
     int left = 0, right = nums.length-1;
     while (left <= right) {
         int mid = left + (right - left) / 2;
         if (nums[mid] < target) left = mid + 1;
         else right = mid-1;
     }
     return right;
 }
```

Leetcode problem: Heaters， Arranging Coins， Valid Perfect Square，Max Sum of Rectangle No Larger Than K，Russian Doll Envelopes, Valid Triangle Number

Find the first value which is larger than the target value/ the last value which is not larger than the target value. This one is similar to the last one.

 int find(int[] nums, int target) {
     int left = 0, right = nums.length-1;
     while (left <= right) {
         int mid = left + (right - left) / 2;
         if (nums[mid] <= target) left = mid + 1;
         else right = mid-1;
     }
     return right;
 }

Leetcode problem: Kth Smallest Element in a Sorted Matrix, Sqrt(x)

There are some other problems which can be solved by binary search as a small part of the solution. And for those difficult problems, the target value may change. The solution to solve these difficult problems depends on different requirements.

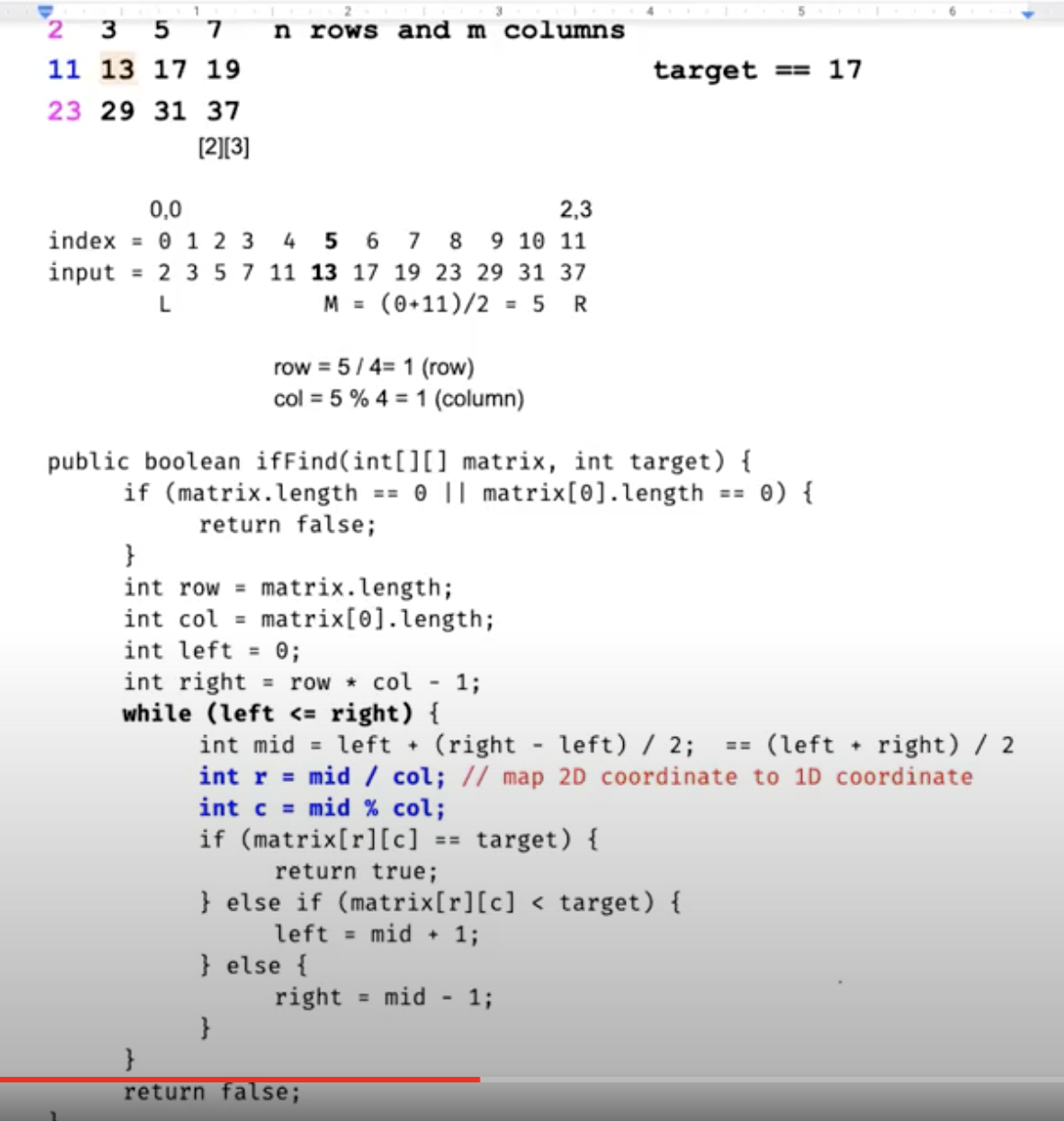
When we try to use binary search on a 2D matrix, there are two ways. One way is use binary search for row and column separately. The other way is treat a 2D matrix as 1D array. Map 2D coordinates to 1D coordinate. RUNOOB game2

Closest Element to Target

RUNOOB game2

Find the first & last target

RUNOOB game2

Closest k Elements

RUNOOB game2

K-th Smallest in two sorted arrays

RUNOOB game2

K-th closest elements

RUNOOB game2

Binary search with unknown size

RUNOOB game2

69. Sqrt(x) (Easy)

This is the second kind of binary search. Find the last value which is smaller than sqrt(target).

Time complexity is O(logx). Space complexity is O(1). Here is the link.

    public int mySqrt(int x) {
        int left = 1;
        int right = x;
        while(left<=right){
            int mid = left+ (right - left) / 2;
            int sqrt = x/mid;
            if(sqrt == mid)return mid;
            else if(mid>sqrt) right = mid-1;
            else left = mid+1;
        }
        return right;
    }

744. Find Smallest Letter Greater Than Target (Easy)

This is the third version of binary search. Find the first value which is larger than the target value. We need to return (right+1), because right means the the last value which is not larger than the target value. And the problems said ‘Letters also wrap around’, so we need to update right if right is equal the length of array.